지난번 포스팅에서는 인턱터와 커패시터에 대한 학습 후, 저항과 결합된 RL, RC 회로들에 대해서 간단히 알아보았다.
#15 기본적인 RL/RC 회로 - 시정수/시상수가 뭘까?
이번 시간엔 기본적인 RL 회로, 즉 저항 R과 인덕터 L이 결합된 회로에 대해 살펴볼 것이다.인덕터와 커패시터에 대한 기본적인 내용은 아래 포스팅을 참고하자. #13 인덕터(Inductor) - 자기장 저장
enfj-electronics.tistory.com
본 포스팅의 제목에서 유추할 수 있겠지만, 이번에는 세 가지 소자가 모두 사용된 회로를 분석해볼 것이다.
저항 R, 인덕터 L, 커패시터 C의 결합인 RLC 회로는 어떤 형식일지 바로 살펴보자.
병렬 RLC 회로

회로 이름에 충실하게 R, L, C가 모두 병렬로 연결되어 있다.
각 소자에 모두 V라는 전압이 할당되어 있고, 각각에 흐르는 전류가 위 사진과 같다.
이때, KCL을 적용해보면 아래와 같이 적을 수 있다.

미분도 있고 적분도 있다니..
보기만해도 더럽다.
식1을 깔끔하게 한 번 더 미분하여 적분항을 소거해본다면, 아래와 같이 표현된다.

일단 V를 구하는 것을 목적으로 할 때, 이에 대한 2차 미분 방정식의 형태가 되었다.
정리된 식은 본인(V)을 여러번 미분한 것들의 합이 0이 되는 형식이다.
따라서 지수 함수를 통해 V를 다음과 같은 형식으로 표현할 수 있다.
(지금부터 기술하는 내용은 공학수학을 수강하면 이해에 도움이 된다.)

A와 s를 미지수로 가정하고 식3을 식2에 대입하면 다음과 같이 정리할 수 있다.

식4의 앞부분인 Ae^st 는 0이될 수 없으므로, s에 대한 2차 방정식이 0이 되어야한다.
이때 s에 대한 2차 방정식을 '특성 방정식'이라고도 한다.
이를 풀면 s는 다음과 같다.

두 해 s1, s2 모두 식3에 적용가능하다.
s1을 대입할 때의 A값을 A1, s2을 대입할 때의 A값을 A2라고 해보자.
당연히 어떤 s값을 적용해도 V의 해가 되므로, 미분방정식의 선형성을 고려할 때 s1, s2를 포함하는 각 근의 합 역시 V의 해가 된다.
따라서 일반적인 V의 형태를 다음과 같이 적을 수 있다.

이제 우리가 모르는 미지수는 A1과 A2 뿐이다.
이를 구하기 위해서는 여기서는 초기값에 대한 정리를 먼저 진행해야 한다.
커패시터와 인덕터는 시간에 따라 전압/전류가 변하는 특성이 있었고, 처음 어느 지점에서 얼만큼의 전압/전류가 흐르는 것이 중요했다.
인덕터의 경우 전류가 급격하게 변하지 않으므로 초기 전류, 커패시터의 경우 전압이 급격하게 변하지 않으므로 초기 전압을 구하는 것이 포인트였다.
#12. 커패시터(Capacitor) - 전하 저장소
여지껏 회로해석의 기초가 되는 소자는 저항이었다.저항은 옴의 법칙에 의거하여 흐르는 전류에 따른 전압이 할당되어 에너지를 소모하는 소자였다면,오늘 살펴볼 커패시터는 에너지를 저장할
enfj-electronics.tistory.com
#13 인덕터(Inductor) - 자기장 저장소
본 포스팅에서는 저항, 커패시터에 이은 새로운 소자, 인덕터(Inductor)에 대해 소개하겠다.이전 커패시터 소개 포스팅을 읽고 온다면 연관된 내용을 잘 이해할 수 있을 것이다. #12. 커패시터(Capaci
enfj-electronics.tistory.com
따라서 초기값에 대한 정리를 먼저 해보자.
인덕터 전류 iL과 커패시터 전압 V의 초기값을 각각 iL(0), V(0)라고 할 때, 다음과 같이 표현할 수 있다.

일반적으로 초기값에 관한 내용은 전압원, 스위치 등의 연결 상태를 고려해 추론할 수 있거나 문제에서 주어지는 경우가 많다.
따라서 식7의 초기값을 안다고 가정해보자.
식6에 t = 0을 대입할 경우, 초기값 V(0)과 같은 형태가 되므로 커패시터 초기 전압을 이용해 A1, A2에 대한 첫 번째 식을 구할 수 있다.
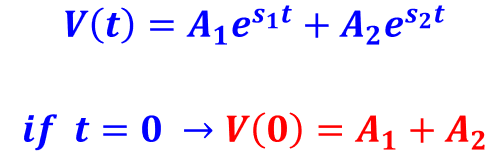
두 미지수의 풀이에 필요한 또 하나의 관계식은 단순한 대입으로는 구할 수 없다.
따라서 조금의 식 변형이 필요하다.
이번에는 식6을 한 번 미분하여 t = 0을 대입해보자.
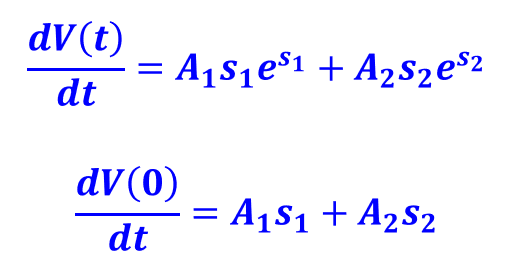
뭔가 뭔가 익숙한 모양이지 않는가?
커패시터 전류는 전압 V(t)의 미분과 커패시턴스 C의 곱으로 표현가능하므로, 커패시터 전류 iC의 형태와 유사하다.
식1에서의 KCL 방정식을 통해 t = 0에서의 식을 정리하면 다음과 같다.
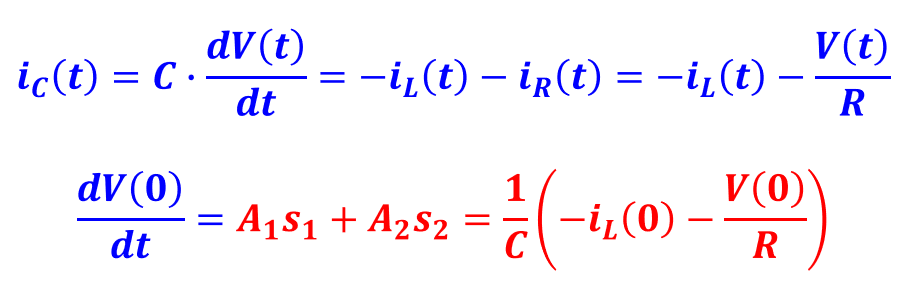
결론적으로 식5에서 구한 s1/s2, 식7에서 구한 초기값을 식8과 식10에서 빨간색으로 표시된 연립 방정식에 대입하면 A1/A2를 구할 수 있다.
꽤나 복잡해보이지만 미분방정식만 가미된 이전의 회로 해석법과 큰 차이가 없긴 하다.
요약하자면 RLC 회로의 해석법은 다음과 같이 정리할 수 있다.
① KCL / KVL을 통해 R,L,C에 대한 미분 방정식을 세운다. ② 미분 방정식의 일반해 형태를 미지수 A, s를 사용하여 잡는다.③ 미분 방정식을 정리하여 s를 먼저 구한다.④ 커패시터와 인덕터의 초기값을 구한다. ⑤ 초기값(t = 0인 시점에서의 값)을 이용하여 일반해 형태의 미지수 A를 구한다.
다음 강의에서는 기본적인 RLC 회로의 해석법을 살펴봤으므로 이를 조금 더 깊숙히 들여다 볼 예정이다.
본 포스팅의 내용을 꼭꼭 숙지해둔다면 이해에 큰 도움이 될 것이다.
오랜만의 포스팅 끝 ~
'회로이론' 카테고리의 다른 글
| #15 기본적인 RL/RC 회로 - 시정수/시상수가 뭘까? (0) | 2024.11.08 |
|---|---|
| #14 인덕터와 커패시터의 직렬/병렬 연결 - 과연 저항과 같을까? (0) | 2024.11.07 |
| #2. 회로기호 / 노드와 브랜치 (Node & Branch) - 회로의 척추 (26) | 2024.11.06 |
| #1. 회로이론 3분 만에 입문하기 - 전하 / 전류 / 전압 / 저항 / 옴의 법칙 (32) | 2024.11.06 |
| #13 인덕터(Inductor) - 자기장 저장소 (38) | 2024.07.05 |



