이번 시간엔 기본적인 RL 회로, 즉 저항 R과 인덕터 L이 결합된 회로에 대해 살펴볼 것이다.
인덕터와 커패시터에 대한 기본적인 내용은 아래 포스팅을 참고하자.
#13 인덕터(Inductor) - 자기장 저장소
본 포스팅에서는 저항, 커패시터에 이은 새로운 소자, 인덕터(Inductor)에 대해 소개하겠다.이전 커패시터 소개 포스팅을 읽고 온다면 연관된 내용을 잘 이해할 수 있을 것이다. #12. 커패시터(Capaci
enfj-electronics.tistory.com
#12. 커패시터(Capacitor) - 전하 저장소
여지껏 회로해석의 기초가 되는 소자는 저항이었다.저항은 옴의 법칙에 의거하여 흐르는 전류에 따른 전압이 할당되어 에너지를 소모하는 소자였다면,오늘 살펴볼 커패시터는 에너지를 저장할
enfj-electronics.tistory.com
RL 회로
백문이불여일견.
바로 예시 회로를 살펴보자.

20 V의 전압원이 t = 0에서 회로에서 Open될 때, 시간에 따라 변화하는 인덕터 전류 IL을 구해보자.
인덕터의 전압은 전류 변화량에 비례하게 되는 특성이 있다. (V = L * dI/dt)
따라서 오랜 시간 스위치가 닫혀 있었다면 인덕터의 전류 변화는 없었을 것이고 단락된 상태로 동작하게 된다.
즉, t = 0 이전에는 20 Ω과 30 Ω만이 연결된 것과 같으므로 초기 인덕터 전류는 1 A가 된다.

이후 20 V 전압원이 막 Open되는 t = 0+ 시점에서, 인덕터 전류 IL이 모든 저항에 흐르게 된다.
또한 인덕터에서는 전류 강하가 발생하지 않으므로 크기는 1 A 그대로이다.

저항 사이의 노드를 V1이라고 가정하고 KVL을 사용하고, V1과 IL의 관계식을 통해 다음과 같이 미분방정식을 세울 수 있다.

마지막 미분 방정식을 만족하는 해를 구하면 각 시간대별 인덕터 전류 IL의 값을 알 수 있다.

사실 미분 방정식을 풀 수 있다는 점에서 공업/공학 수학 선행이 필요한 부분이다.
여유가 된다면 포스팅 후 링크를 걸어두겠다.
RC 회로
이전 내용에서 살펴본 것 처럼 RC 회로 역시 여태 배운 회로 해석법을 커패시터와 적용한다.
이 과정에서 미분방정식의 해를 구하는 형태로 진행되는 것은 동일한다.
마찬가지로 예시 회로를 살펴보자.

10 V의 전압원과 4 Ω을 통해 연결되어 있다가, 이후엔 2 Ω과만 연결되는 형태이다.
이때 시간에 따른 커패시터 전압 Vc를 구해보자.
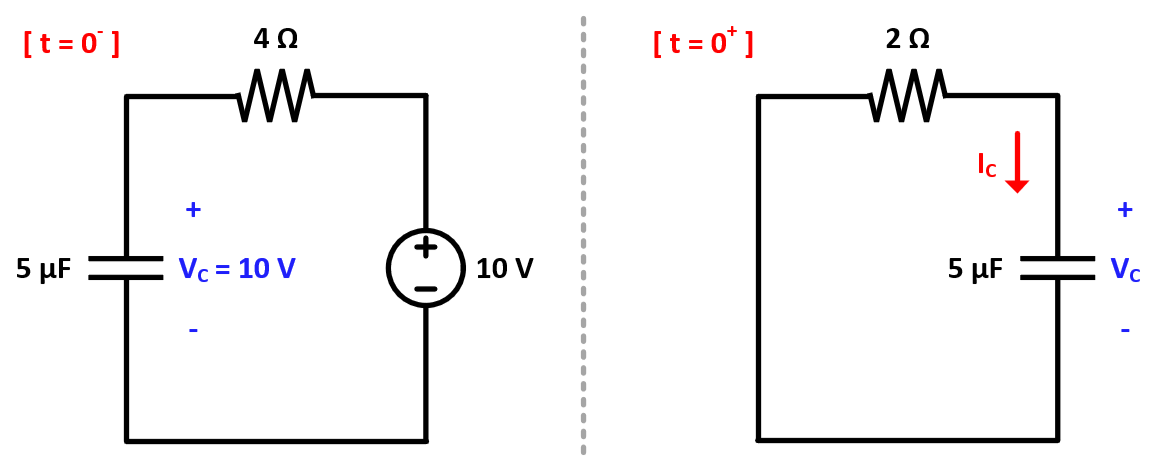
먼저 t = 0-에서는 완충된 커패시터에 10 V가 인가되어 있을 것이다.
시간이 조금 지나 스위치의 방향이 변하고 t = 0+가 되더라도, 커패시터에서는 순간적인 전압 강하가 없으므로 Vc는 10 V가 된다.
또한 2 Ω과 커패시터 모두 Ic만큼의 전류가 흐른다고 잡고 KVL을 적용하면 다음과 같이 표현할 수 있다.

상기 미분방적식의 해를 구해 이를 만족하는 Vc를 찾으면 다음과 같다.

초기 전압 10V에서 시작하여 점점 방전되는 모습을 볼 수 있다.
t = 0+에서부턴 전원 공급 없이 저장된 에너지를 방전하면서 지수 함수의 형식으로 저항에 에너지를 공급하고 있는 모습을 뜻한다.
시간이 지나 충전된 모든 전하가 흘러 나간다면 결국 0 V에 도달하는 것이다.
τ (타우) : 시상수, 시정수, 시간 상수
상기 예시들을 풀어보며 조금은 RL, RC 회로에 친숙해졌으리라 믿는다.
이번에는 특정한 소자 값이 아닌 일반적인 RL, RC 회로에서의 문제해결을 살펴보겠다.
아래와 같은 두 회로에서 파란색으로 표기된 IL, VC를 각각 구해보자.
(지난 포스팅에서 본 회로와 같다.)

각각 KVL을 적용하여 미분방정식을 풀어보면 아래와 같은 해를 얻을 수 있다.

이때 빨간색으로 표시된 상수에 집중하자.
이들은 자연 상수 e의 지수 형태에서 시간 변수 t와의 비율을 나타낸다.
그래프의 형태를 보면 인덕터와 커패시터에서의 방전 속도를 결정함을 알 수 있다.
(만약 충전되는 형태의 회로였다면 충전 속도일 것이다.)
즉, 시간 t에 따라 충/방전 속도를 나타내는 계수 이를 시간과 관련된 상수이다.
이때 지수의 분모가 1이 되게 하는 값이 τ (타우)이다.
τ (타우)는 시상수, 시정수, 시간 상수 등으로 불린다.
그렇다면 시상수 τ의 물리적인 의미는 무엇일까?

만약 t = τ 인 시점에서는 K에서 시작하는 특정 함수가 1/e배 감쇠되어 초기값 대비 약 0.37배 되었다는 뜻이 된다.
t = 2τ라면0.14K, t = 3τ에서는 0.05K, t = 5τ에서는 0.01K가 된다.
즉, 시상수 대비 시간으로 최종값에 얼마나 근접했는지가 표현된다.
이번에는 방전이 아닌 충전 함수를 살펴보자
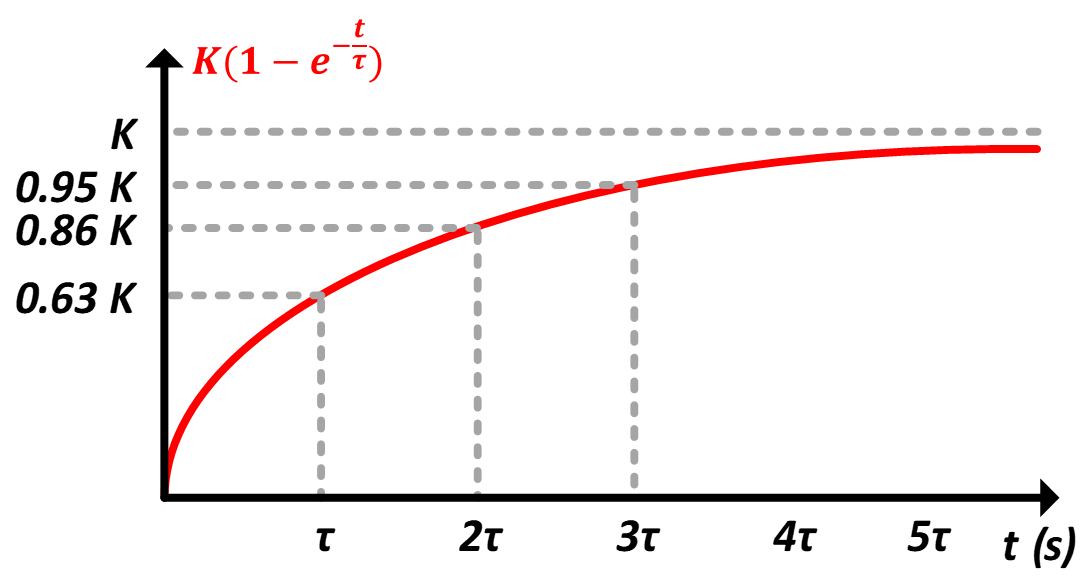
0에서부터 시작하여 최종적으로는 K라는 값에 도달할 것이다.
t =τ라면 0.63K, t =2τ라면0.86K, t = 3τ에서는 0.95K, t = 5τ 에서는 0.99K가 된다.
요약하자면 시간을 시상수의 비로 표현한다면 최종값에 얼마나 근접했는지를 표현할 수 있다.
주로 최종값 대비 5%의 오차를 보이는 3τ, 1%의 오차를 보이는 5τ 값을 주로 사용한다.
예를 들어 t = 5τ라면 '아~ 최종값과 1% 이내의 오차만 나타날 정도로 시간이 흘렀구나~' 라고 이해하면 된다.
오늘은 기본적인 RL, RC 회로와 시정수(시상수, 시간상수) 타우에 대해 알아보았다.
그 다음 내용인 RLC 회로를 쉽게 이해하기 위해선 선행되어야 하는 내용이 많다.
어떤 식으로 풀어나갈지 벌써부터 고민이지만..
고민은 나의 몫.
여러분은 쉽게 이해만 해줬으면 좋겠다.
오늘의 포스팅 끝~
'회로이론' 카테고리의 다른 글
| #16. RLC 회로 (1) - 2차 미분방정식 풀기 (0) | 2025.03.02 |
|---|---|
| #14 인덕터와 커패시터의 직렬/병렬 연결 - 과연 저항과 같을까? (0) | 2024.11.07 |
| #2. 회로기호 / 노드와 브랜치 (Node & Branch) - 회로의 척추 (26) | 2024.11.06 |
| #1. 회로이론 3분 만에 입문하기 - 전하 / 전류 / 전압 / 저항 / 옴의 법칙 (32) | 2024.11.06 |
| #13 인덕터(Inductor) - 자기장 저장소 (38) | 2024.07.05 |



