앞서 포스팅한 새로운 수동 소자 인덕터, 커패시터를 제대로 이해했는가?
이번 시간에는 이들의 직렬 연결과 병렬 연결에 대해 살펴볼 예정이다.
기존에는 저항만을 가지고 각 연결 별로 등가저항을 구해봤지만, 기억이 안 난다면 잠시 되새김질을 하고 오자.
#4. 직렬 연결과 병렬 연결 - 릴레이와 트랙
중고등학교 때 간단하게나마 직렬 연결과 병렬 연결을 접해보았을 이가 많을 것이다. 배터리를 병렬 연결할 경우 전구가 오래가고~ 직렬 연결을 하면 전구의 빛이 밝아진다나 뭐라나~ 오늘은 직
enfj-electronics.tistory.com
이전에도 말한 내용이지만, 아래 내용은 꼭 기억하자.
병렬 연결은 같은 노드에 연결되어 같은 전압을 공유한다.
직렬 연결은 브랜치가 연속적으로 연결되어 같은 전류를 공유한다.
기본적인 이전 내용은 이해했다는 가정 하에 급하신 분들을 위한 요약을 먼저 진행한 후 시작하겠다.
| 직렬 (Series) 연결 | 병렬 (Parallel) 연결 | |
| 인덕터 (Inductor) | 저항의 직렬과 같음 | 저항의 병렬과 같음 |
| 커패시터 (Capacitor) | 저항의 병렬과 같음 | 저항의 직렬과 같음 |
아무래도 최근에 배운 인덕터와 커패시터와 달리 익숙한 소자인 저항과의 비교를 곁들였다.
자세한 원리를 살펴보기 위해 포스팅을 시작하겠다.
인덕터의 직렬 연결
아래 그림과 같이 직렬로 연결된 인덕터가 n개 있는 상황을 가정해보자.

각 인덕터에는 모두 같은 전류가 흐르므로 KVL을 적용해본다면 다음과 같이 적을 수 있다.

(어째서 위와 같은 식이 나오는지 이해가 안된다면.. 돌아가자..↓)
#13 인덕터(Inductor) - 자기장 저장소
본 포스팅에서는 저항, 커패시터에 이은 새로운 소자, 인덕터(Inductor)에 대해 소개하겠다.이전 커패시터 소개 포스팅을 읽고 온다면 연관된 내용을 잘 이해할 수 있을 것이다. #12. 커패시터(Capaci
enfj-electronics.tistory.com
등가 저항을 구할 때와 마찬가지로 여러 인덕터의 직렬 연결을 간소화하여 등가 인덕터 하나로 표현한다면, 다음과 같이 표현할 수 있다.

따라서 등가 인덕턴스 Leq는 아래와 같이 표현할 수 있다.

수식적인 표현이 아니라 직감적으로 이를 이해하려면, 인덕터는 기본적으로 전류의 흐름 방해하는 특성이 있다는 것을 상기해보자.
인덕턴스가 커질수록 같은 전압일 때, 전류의 변화를 억제한다.
이는 곧 저항과 비슷한 특성을 가진다는 것을 알 수 있다.
실제로 직렬 등가 인덕턴스 식과 직렬 등가 저항 식을 비교해보면 이를 더 명확하게 알 수 있다.
인덕터의 병렬 연결
이번엔 병렬로 연결된 n개의 인덕터를 떠올려보자.

전압이 V인 위쪽 노드에서 KCL을 적용해보면 아래와 같이 쓸 수 있다.

위와 같은 난잡한 식을 간소화하기 위해 등가 인덕턴스를 구하는 회로를 그려본다면 아래와 같다.

등가 인덕턴스는 아래 식과 같다.

눈썰미가 있는 독자들이라면, 저항의 병렬 연결과 형태가 유사한 식임을 알 수 있다.
종합적으로 본다면 인덕터는 저항과 같은 등가식을 가진다라고 이해하면 편하다.
커패시터의 병렬 연결
이번엔 커패시터의 병렬 연결을 살펴보자.
마찬가지로 n개의 커패시터를 병렬로 연결했을 때를 가정해보자.

인덕터 때와 마찬가지로 KCL을 적용해본다면 아래와 같은 식을 세울 수 있다.

(위의 식이 와닿지 않는다면 다시 한 번 정독하고 와보자 ↓)
#12. 커패시터(Capacitor) - 전하 저장소
여지껏 회로해석의 기초가 되는 소자는 저항이었다. 저항은 옴의 법칙에 의거하여 흐르는 전류에 따른 전압이 할당되어 에너지를 소모하는 소자였다면, 오늘 살펴볼 커패시터는 에너지를 저장
enfj-electronics.tistory.com
다시 한번 등가 커패시턴스를 구하기 위한 회로를 그려본다면 아래와 같다.

양 변의 미분항을 소거하여 등가 커패시턴스 Ceq를 구해보면 아래와 같이 표현할 수 있다.

어라라?
병렬 상태의 커패시턴스를 정리해보면 저항과 인덕터의 직렬 연결 상태의 식과 같은 형식임을 알 수 있다.
병렬로 연결하는 커패시터가 늘어날수록 더 커지는 커패시턴스를 갖는다.
이는 커패시턴스라는 지표와 커패시터의 구조를 상기해보면 직관적으로 알 수 있다.
전하를 저장할 수 있는 능력을 나타내므로, 평행판 구조의 전하 보관소를 병렬적으로 연결할수록 더 많은 전하 수용 능력을 띈다고 이해하면 된다.
커패시터의 직렬 연결
마지막은 커패시터 n개의 직렬 연결이다.
이쯤되면 슬슬 감을 익혔을테지만 친절한 나는 상세히 살펴보겠다.

모든 커패시터들은 전류 I를 공유한다는 것을 명심한 채 KVL을 적용한다면, 아래와 같은 식을 세울 수 있다.
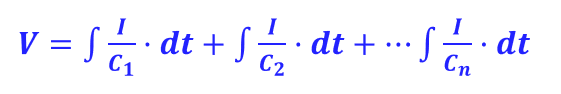
직렬 커패시터들과 동일한 역할을 하는 등가 커패시터 하나로 표현한다면 아래와 같다.

적분 안쪽 같은 항들을 묶어 간소화 한다면, 아래와 같이 등가 커패시턴스를 구할 수 있다.

상기 식은 간단한 값을 대입해보면 알 수 있겠지만, 커패시터를 직렬 연결할 경우 등가 커패시턴스는 오히려 줄어드는 것을 알 수 있다.
엥? 직관적으로 와닿지 않는다.
왜 직렬로 쌓으면 기존보다 낮은 전하 저장 능력을 보이는 것일까?
일단 아래와 같이 직렬 커패시터 회로에서 전압원 V가 Q만큼의 전하를 전달하는 상황을 떠올려보자.

C1의 좌측에 +Q만큼의 전하가 전달된다고 가정해보자.
그렇다면 전기적 중성을 맞추기 위해 C1의 우측에는 -Q만큼의 전하가 움직여야 한다.
이는 C2의 좌측 면에 +Q만큼의 전하가 다시 전달되었음을 의미한다.
만약 직렬로 연결된 특정 커패시터 중 Q만큼의 전하를 보유/전달할 수 없다면 더 이상 전하는 전달되지 않는다.
즉, 가장 낮은 커패시턴스를 갖는 소자에 등가 커패시턴스가 큰 영향을 받는다는 뜻이다.
가령 2인3각 달리기를 한다고 가정한다면 둘의 속도는 빠른 쪽이 아닌 느린 쪽에 맞출 수 밖에 없다는 것을 떠올려도 된다.
위와 같은 전하 전달 매커니즘을 이해했다면 직렬 연결에서의 커패시턴스를 직관적으로 받아드리는 것에 큰 도움이 될 것이다.
※ 위 구매 링크는 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다.
'회로이론' 카테고리의 다른 글
| #16. RLC 회로 (1) - 2차 미분방정식 풀기 (0) | 2025.03.02 |
|---|---|
| #15 기본적인 RL/RC 회로 - 시정수/시상수가 뭘까? (0) | 2024.11.08 |
| #2. 회로기호 / 노드와 브랜치 (Node & Branch) - 회로의 척추 (26) | 2024.11.06 |
| #1. 회로이론 3분 만에 입문하기 - 전하 / 전류 / 전압 / 저항 / 옴의 법칙 (32) | 2024.11.06 |
| #13 인덕터(Inductor) - 자기장 저장소 (38) | 2024.07.05 |



