키르히호프의 전압과 전류 법칙
이전 글에서 노드와 브랜치의 개념을 이해했다면, 이번 포스팅의 주제인 키르히호프의 법칙에 쉽게 다가갈 수 있다.
키르히호프의 법칙은 복잡해 보이는 회로를 분석하는 데 있어 기초적이면서 강력한 도구이다. 그럼에도 매우 쉽다.
딱 두 가지만 기억할 것.
① 노드마다 특정 전압이 할당되어 있다.
② 노드에서 들어오고 나가는 전류의 합은 같다. (= 들어오는 전류의 합은 0이다, 나가는 전류의 합은 0이다.)
나는 똑똑하지 않고 암기를 싫어해서, 직관적이지 못한 표현을 아주 싫어한다.
속칭 '먹물'식 표현으로는 아래와 같이 정의하기도 하지만,

(대충 폐루프 내에서 전위차의 합은 0이라는 뜻)

(대충 노드로부터 뻗어나가는 브랜치들로 흐르는 전류의 합은 0이라는 뜻)
보자마자 거부감이 들고 읽기 싫어진다. 메스껍다.
필자가 말한 두 가지 표현을 아래의 예시를 통해 살펴보자.
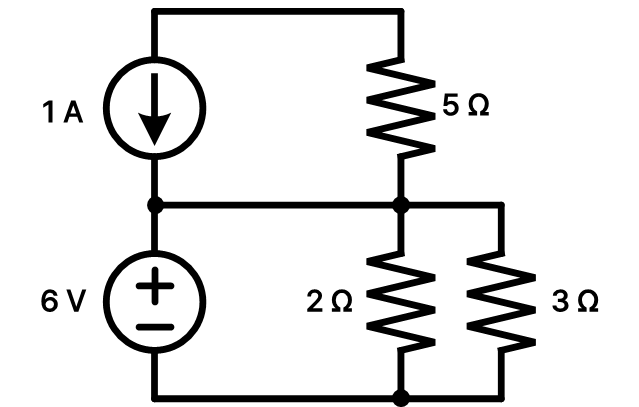
이전 포스팅에서 본 예시와 비슷한 회로이다.
(귀찮아서 그런 건 절대 아니다. 독자들에게 익숙한 예시를 들고 왔을 뿐)
보자마자 노드와 브랜치가 각각 3개 / 5개인 것을 부디 알아챘길 바란다.
(모르겠으면 돌아가라 ↓)
#2. 회로기호 / 노드와 브랜치 (Node & Branch) - 회로의 척추
회로에 대한 본격적으로 알아보기 전 노드(Node)와 브랜치(Branch)에 대한 개념을 알아야 한다. 이에 앞서 기본적인 회로 기호들에 대해 알아보자.회로 기호우리에게 흔히 '회로'라고 치부되는 초
enfj-electronics.tistory.com
키르히호프 전압 법칙
일단 상술한 ① 노드마다 특정 전압이 할당되어 있다. 를 살펴보자.
3개의 노드에 각각 특정 전압이 할당되어 있다는 의미이다.
이때, 독립전압원 6 V가 의미하는 것은, 위쪽 (+) 노드와 아래쪽 (-) 노드 사이의 전압(=전위차)가 6 V라는 말이다.
편의상 아래쪽 노드를 0 V라고 가정한다면, 전압원 바로 위쪽 노드는 6 V가 되는 것이다.
그렇다면 전류원이 연결된 최상단 노드의 전압은? 아직 모른다. 쫌 기다려 봐라.

키르히호프 전류 법칙
이때 두번째 법칙, ② 노드에서 들어오고 나가는 전류의 합은 같다. 를 사용한다.
물음표로 표시된 최상단 노드의 경우, 2개의 브랜치(1 A 전류원과 5 Ω 저항)과 연결되어있다.
전류원을 통해 나간 1 A의 전류는, 5 Ω의 저항을 통해 들어오고 있는 것이다.
첫 번째 포스트에서 본 옴의 법칙은 기억나는가? V = IR. 전압은 전류와 저항의 곱이다. 이걸 써먹을 때가 왔다.
5 Ω 저항에 1 A의 전류가 흐른다면? 전압은 5 V가 된다. 여기서 말하는 '5 V'는 두 노드 간의 전압 차이를 의미한다.
이때 5 Ω 저항 기준 전류의 방향은 위쪽 노드로 들어가는 방향으로 흐르고, 전류는 전압이 높은 곳에서 낮은 곳으로 흐르므로 중간쪽 노드가 위쪽 노드보다 5V 높다라는 것을 알 수 있다.
즉, 중간 6 V 노드보다 상단 노드의 전압이 5 V 낮으므로, 상단 노드의 전압은 1 V가 된다.
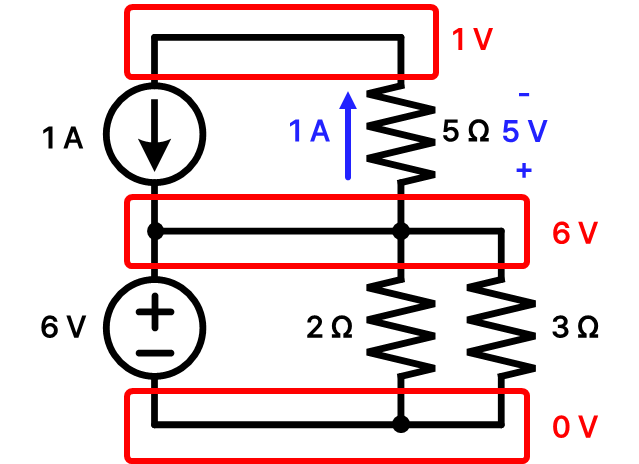
노드별 전압을 다 구했다면? 거의 다 끝났다. 각 노드별 모든 전압과 각 브랜치별 모든 전류를 파악한다면, 회로를 공략했다고 생각하면 된다.남은 브랜치들의 전류를 파악해보자.
2 Ω 저항의 경우 위쪽엔 6 V, 아래쪽엔 0 V가 할당되어 있다. V = IR = 6 = 2I, 전류는 3A가 되고, 방향은 위에서 아래이다.
3 Ω 저항도 마찬가지로 계산해보면 2 A의 전류가 위에서 아래로 흐르는 것을 알 수 있다.

이제 전압원에 흐르는 전류만이 남았다.
최하단 0 V 노드를 살펴보면 3개의 브랜치와 연결되어 있는데, 2 Ω과 3 Ω 저항을 통해 총 5 A의 전류가 들어오고 있다.
들어온게 있으면 나가는 것도 있어야겠지?
들어온 5 A의 전류는 6 V 전압원을 통해 빠져나가게되고, 방향은 아래에서 위다.
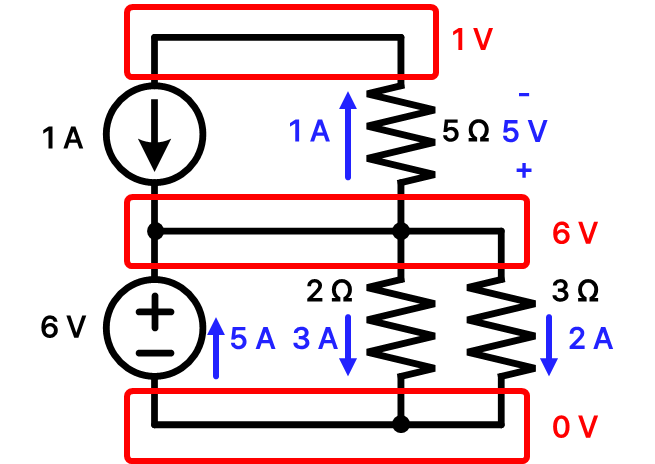
중간 6 V 노드에서 전류의 흐름을 살펴봐도 전압원과 전류원을 통해 들어오는 전류 1 A, 5 A와 세 저항을 통해 빠져나가는 전류 1 A, 2 A, 3 A의 합이 같음을 알 수 있다.
이제 모든 소자들 사이의 전압과 전류를 분석이 끝났다.
방정식에선 미지수 x를 구하면 '풀었다'고 표현하듯, 모든 소자들에 흐르는 전압과 전류 분석이 끝난 것을 회로를 '해석했다'고 표현한다.
Path와 Loop
여태했던 내용을 정리하면서 포스팅 제목인 'N빵'의 의미를 되짚어보자.
각 노드는 '전압'을 할당받고, 각 브랜치는 '전류'를 할당받는다.
그리고 이는 N빵(속칭 뿜빠이)과 같이 아주 공평하다.
노드에서 뻗어나간 브랜치들의 전류는 출입량이 같다.
전압의 경우도 이와 같은 공평함을 갖는데, 이는 패스(Path)와 루프(Loop)라는 개념을 알 필요가 있다.
패스는 쉽다. 아무 노드에서 시작해서 브랜치들을 갯수 상관없이 겹치지 않고 연결해보아라.
가능한 모든 경우의 수가 패스가 된다. 인생을 어떻게 살아가더라도 다 길(Path)이 있다는 교훈을 준다.

그리고 패스 중, 시작하는 노드와 끝나는 노드가 같은 패스를 루프라고 한다.

어떤 루프를 지나가더라도 각 소자를 지나가며 전압 변화의 합을 살펴보면 0이 되는 것을 알 수 있다.
이것이 포스팅 초반 수식으로 나타냈던

의 물리적 의미이다.
조금 높이 있는 것 같더라도 (= 전압이 높은 것 같더라도) 돌아오면 제자리이다.
높은 전압이라도 여러 소자를 거치며 제자리로 돌아왔을 때는 그대로이고, 많은 전류가 들어오더라도 나가는 양과 비교하면 남는 게 없다. 회로는 아주 공평하다. 세상과는 다른 유토피아랄까? 나는 회로가 참 좋다.
.
.
.
로 포스팅을 끝내기엔 이해가 잘 안갈 수도 있을 것 같아, 두 번째 예시 회로를 남기겠다. 알아서 해석해보도록.

모든 노드의 전압과 브랜치들에 흐르는 전류와 방향을 찾아보자.
.
.
.
똑
딱
똑
딱
.
.
.
시계는 와치
시계는 와치
.
.
.
똑
딱
똑
딱
.
.
.

본인의 답과 일치한다면, 축하한다 ! 잘 이해한 것이다.
이해가 안되는 부분이 있다면 위로 다시 올라가서 차분히 이해해보도록 하자.
(그래도 모르겠다면 댓글로 남겨주라.)
근데 오늘의 포스팅을 자세히 이해했다면 드는 의문점들이 몇 개 있을 것이다.
'전류는 전압이 높은 곳에서 낮은 곳으로 흐른다하였는데, 전압원과 전류원에서는 그렇지 않다는 것이 미심쩍다.
이를 설명하기 위해선 능동소자와 수동소자 간의 구분이 필요하다.
결론적으로 전압원과 전류원은 능동소자이므로 전압과 전류의 방향성에 대해 예외적으로 동작하는 것이고,
수동소자인 저항은 고전압에서 저전압으로 전류가 흐른다.
추후 이에 대해 본격적으로 서술해보겠다.
+ 앞으로는 키르히호프의 전압/전류 법칙은 편의상 KVL / KCL 이라고 칭하겠다.
(Kirchhoff's Voltage Law / Kirchhoff's Current Law)
이상 ! 읽어줘서 감사하다.
※ 위 구매 링크는 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다.
'회로이론' 카테고리의 다른 글
| #7. 테브난/노턴 등가회로 - 위정척사 (38) | 2024.06.04 |
|---|---|
| #6. 중첩원리와 전원의 등가회로 - 엄마, 용돈을 왜 그렇게 주시나요? (42) | 2024.06.03 |
| #5-1. 단락(Short)과 개방(Open) - 끊을까? 이을까? (37) | 2024.05.13 |
| #5. 노드 해석법과 메쉬 해석법 - 회로도 번역하기 (38) | 2024.05.12 |
| #4. 직렬 연결과 병렬 연결 - 릴레이와 트랙 (36) | 2024.05.10 |



