Superposition 이라고도 부르는 중첩원리 는 비교적 생소한 용어일 것이다.
이는 선형 시스템에서 나타나는 원리이지만.. 선형 시스템이라는 표현도 낯설다.
처음 접하는 이들의 마음에 깊이 공감하며 비유를 들어보겠다.
부모님 두 분으로부터 용돈을 받는 학생 A을 생각해보자.
하루는 아버지께 용돈 5만원을 받았다.
이후 어머니도 용돈을 준다고 하시길래, 아버지께서 주신 액수와 같은 5만원을 기대하였다
어머니는 이렇게 말씀하셨다.
"아까 아빠가 5만원 줬지? 이미 용돈 받았으니까 3만원만 줄게 ~"
'ㅂㄷㅂㄷ' (사실 필자는 부들부들하지 않다. 용돈을 준다는 사실에 감사해라.)
아버지가 나에게 용돈을 주셨다는 사실이
어머니로부터 받을 용돈 액수 산정에 영향을 준 것이다.
??? : 어머니는 어머니고 아버지는 아버지인데 !!! 그런게 어딨어요?
공학적인 관점에서 봤을 때, 어머니와 아버지는 부부라는 깊은 상관 관계에 놓여있다.
서로가 자식에게 주는 용돈에 있어서 영향을 주고 받는 관계인 것이다.
만약 이 부부가 상대방이 자식에게 얼마의 용돈을 주었든 상관없이 본인이 원하는 액수를 준다면,
어머니와 아버지는 독립적이라고 볼 수 있는 것이다.
이때, 내가 받은 용돈의 총합은 어머니와 아버지로부터 받은 각각의 금액을 가산하면 알 수 있다.
즉, 회로적으로 본다면 여러 독립된 전원(용돈 공급원 = 부모님)으로부터 에너지(용돈)를 공급받는 수동적인 소자(나)가 받는 전력(용돈의 총 합)이 각각의 가산으로 표현된다면 이는 '중첩원리 ' 가 적용된다 라고 표현하다.
잘 이해가 안되더라고 상관 없다. 일단은 이 정도 느낌만 이해하자.
앞서 잠시 언급한 선형 시스템의 경우 중첩 원리를 항상 적용할 수 있다.
이는 선형대수학이나 LTI 시스템을 배우면 알 수 있는데 자세한 건 다음에 설명하겠다.
일단 회로이론 강의에서는 항상 써먹을 수 있다고 생각하면 된다.
(회로이론에서는 수동 소자만 다루기 때문 ! 전자회로나 반도체 분야에서 능동 소자를 배우고나면 추후 설명 예정)
이제 중첩원리를 집중적으로 살펴보자.
중첩의 원리
회로이론에서 중첩의 원리는 딱 2가지만 기억하면 된다.
① 여러 개의 독립 전원이 있을 때 사용할 수 있다.
② 특정 소자에서의 응답은 각각의 독립 전원에 의한 개별 응답의 합으로 나타난다.
이때 응답이란 전기 신호의 제공으로 발생하는 전압이나 전류 등의 반응을 뜻한다.
말로는 잘 이해가 안되지 않는가?
(이해가 된다면 내 블로그말고 전공 서적이나 교수님의 전문적 강의를 봐라.
당신과 같은 인재를 위한 포스팅이 아니니까 ㅎㅎ,,)
예시를 살펴보며 위 설명을 음미해보자.

예시 회로에서 2 Ω에 걸리는 전압과 흐르는 전류를 살펴보자.
일단 독립 전원 2개가 있는 것을 알 수 있다.
각각의 독립 전원이 소자(저항)에 미치는 영향이 독립적이라고 설명했으므로, 개별 전원이 하나씩만 존재할 경우를 살펴보자.
5V 전압원만 존재하는 회로는 어떤 형태일까?
전류원은 효력을 발휘 하지 못할 것이다.
전류가 공급이 되지 않는 Open된 회로일 것이므로 5A 전류원을 개방할 경우, 아래와 같이 볼 수 있다.
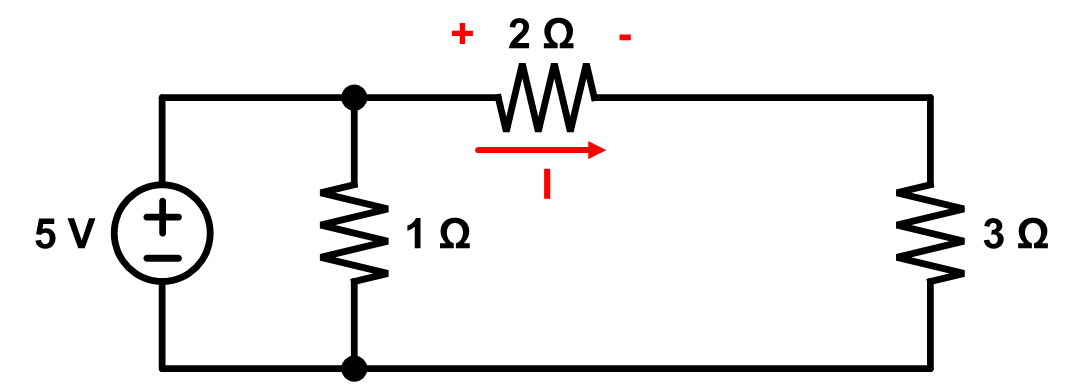
이때, 2 Ω과 3 Ω 저항은 직렬 연결, 그것들과 1 Ω 저항은 병렬 연결이다.
(이해가 안되면 다시금 돌아가자 ↓)
#4. 직렬 연결과 병렬 연결 : 릴레이와 트랙
중고등학교 때 간단하게나마 직렬 연결과 병렬 연결을 접해보았을 이가 많을 것이다. 배터리를 병렬 연결할 경우 전구가 오래가고~ 직렬 연결을 하면 전구의 빛이 밝아진다나 뭐라나~ 오늘은 직
enfj-electronics.tistory.com
따라서 직렬 연결된 2 Ω과 3 Ω 저항을 통해 1 A의 전류가 흐를 것이고, 이때 2 Ω 저항에 걸리는 전압은 왼쪽에서 오른쪽으로 2 V이다.

이번엔 전압원 없이 5 A 전류원만 존재한다고 생각해보자.
전압원이 위 회로에서 효력을 발휘하지 못한다면, 양단에 전위차가 존재하지 않을 것이다. (0 V)
즉, Short된 상황을 의미하므로 예시 회로에서 전압원을 단락시켜본다.

이 경우 위에서 아래로 흐르는 5 A의 전류는 왼쪽과 오른쪽 중 저항성에 따라 분배가 될 것이다.
어디로가지~
이전 포스팅에서 단락을 제대로 이해했다면 1 Ω이 무의미한 저항인 것은 바로 판단되었을 것이다.
#5.5 단락(Short)과 개방(Open) - 끊을까? 이을까?
물이 흐르는 수로를 생각해보자. 서로 다른 물줄기를 수로를 이어버린다면? 물줄기가 하나가 되어 흐른다. 반대로 물이 잘 흐르고 있는 수로를 막아버린다면? 원래 흐르던 방향으로 물이 흐르지
enfj-electronics.tistory.com
5 A의 전류가 2 Ω과 3 Ω을 통해 분배되고, 이 때 두 저항은 병렬 연결이므로 같은 전압이 걸려 있다.
옴의 법칙에서 같은 전압일 때, 저항과 전류는 반비례하므로 2 Ω에는 3 A, 2 Ω에는 2 A의 전류가 흐른 다는 것을 알 수 있다.
또한 2 Ω에 걸리는 전압은 6 V라는 것 또한 알 수 있다.

이제는 중첩의 시간이다.
각 전원들만 존재할 때 연산했던 것을 합쳐서 생각해보자.
전압원만 존재했을 때 2 Ω에 걸리는 전압/전류는 좌측에서 우측 기준 2V, 1A
전류원만 존재했을 때 2 Ω에 걸리는 전압/전류는 좌측에서 우측 기준 6V, 3A
따라서 모두 두 전원이 모두 존재할 경우에 2 Ω에 걸리는 전압/전류는 좌측에서 우측 기준 8V, 4A임을 알 수 있다.
이것이 중첩원리이다.

기존에 배운 회로해석법인 마디해석법/메쉬해석법으로 연산해보더라도 같은 답을 얻을 것이다.
못믿겠으면 확인해보자 ㅎㅎ,, ↓
#5. 회로도 번역하기 : 마디 해석법과 메쉬 해석법
내가 모르는 언어로 작성된 글을 이해할 수 있는 언어로 옮기는 것을 번역이라고 한다.즉, 번역은 알기 쉽게 변환하는 것이다.오늘 배워볼 마디 해석법과 메쉬 해석법은 복잡한 회로도를 쉽게 '
enfj-electronics.tistory.com
여러 회로의 해석에 사용되는 중첩 원리를 살펴보았다.
독립 전원이 아닌 종속 전원을 따로 제거하는 실수를 범하지 않는다면, 매우 유용한 해석 기법이다.
오늘 포스팅은 여기까지.
오랜만에 포스팅을 작성하니 뭔가 어색하다.
앞으로도 틈틈히 올려보겠도다.
※ 위 구매 링크는 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다.
'회로이론' 카테고리의 다른 글
| #8. 교류(AC)와 직류(DC) - E와 I (MBTI) (34) | 2024.06.09 |
|---|---|
| #7. 테브난/노턴 등가회로 - 위정척사 (38) | 2024.06.04 |
| #5-1. 단락(Short)과 개방(Open) - 끊을까? 이을까? (37) | 2024.05.13 |
| #5. 노드 해석법과 메쉬 해석법 - 회로도 번역하기 (38) | 2024.05.12 |
| #4. 직렬 연결과 병렬 연결 - 릴레이와 트랙 (36) | 2024.05.10 |



