앞서 살펴본 연산 증폭기의 원리를 토대로 다양한 회로를 구성해볼 것이다.
#9. 연산 증폭기 (OP-Amp) - 신호 돋보기
오늘은 연산증폭기라고 하는 새로운 소자에 대해 알아볼 것이다.전공자들은 주로 OP-Amp ('오피 앰프'라고 읽으면 됨)라고 부르는 이 놈 !회로관련 과목 뿐만 아니라 통신, 제어 등 다양한 분야에
enfj-electronics.tistory.com
면밀하게 이해가 되었다면, 회로의 만능 재료인 연산증폭기를 활용하여 다양한 요리를 선사해보이겠다.
코스의 순서는 반전 증폭 회로, 비반전 증폭 회로로 진행하겠다.
(사실 더 많았는데 포스팅이 너무 길어져서 나눔 ㅎㅎ,,)
반전 증폭 회로 (Inverting Amplifier Circuit)
'반전' 증폭 회로는 이름에서 유추할 수 있듯 신호가 반전되게 증폭되는 회로이다.
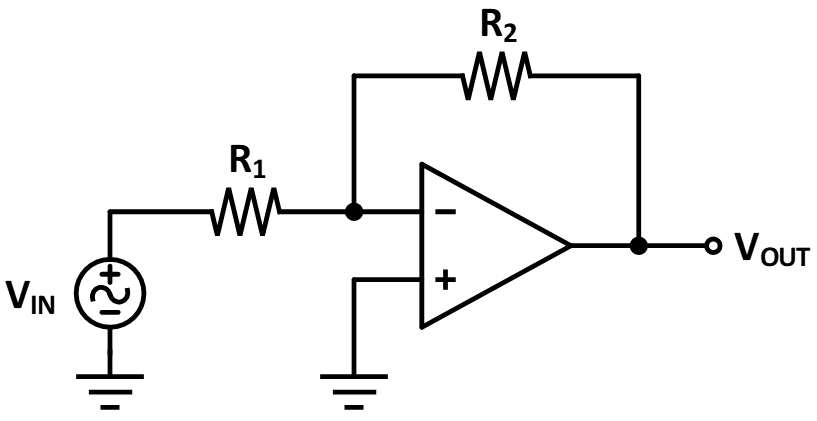
간단한 반전 증폭 회로는 위 사진과 같이 -입력단에 입력 신호가 연결된 모습이다.
입력 신호 Vin과 저항 R1과 R2를 위와 같이 연결시킨 경우 출력 전압 Vout은 어떻게 되는지 살펴보자.
먼저 연산증폭기의 +입력단이 그라운드와 연결되어있으므로 -입력단 또한 같은 전압을 가질 것이다.
이때, R1의 양단에는 Vin과 0 V가 할당되어있으므로 R1에 흐르는 전류 I = Vin / R1이 된다.
그렇다면 R1을 통과한 전류 I는 어디로 흘러 들어갈까?
이전 포스팅에서 연산증폭기의 입력 임피던스는 엄~청 크다는 것을 기억하는가?
해당 특성으로 인해 입력단자는 Open과 같이 동작하므로 전류가 흘러들어가지 않고, I는 그대로 R2에 흐르게 된다.

R2에 할당되는 전압은 I·R2가 될 것이고 Vout에 걸리는 전압은 R2와 R1의 비에 따라 나타나고 부호는 마이너스, 즉 입력신호와 반대 방향이 되어 반전된다.
이 회로에서 전압 이득 (= 입력 신호대 출력 신호의 비, Vin과 Vout의 비)를 살펴보면 아래와 같이 표현할 수 있다.

비반전 증폭 회로 (Non-inverting Amplifier Circuit)
이번엔 비반전 증폭 회로.
앞선 반전 회로와 달리 입력 신호가 반전되지 않고 출력 신호로 내뱉는 회로임을 유추할 수 있다.
바로 예시를 살펴보자.
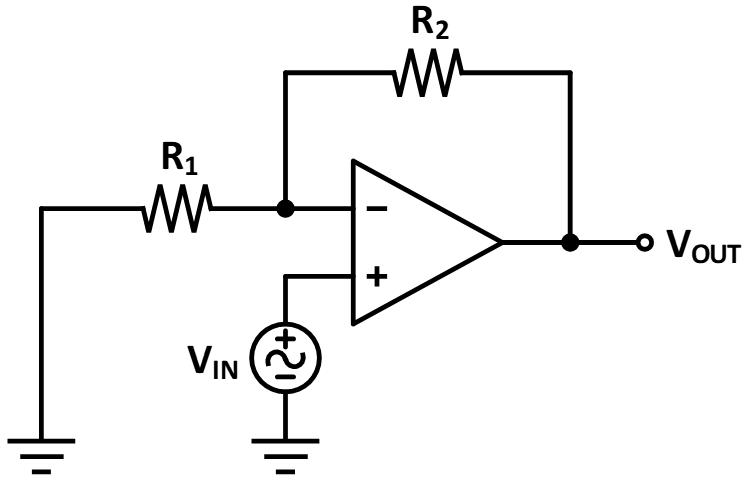
제일 먼저 +입력단에 입력 신호가 연결된 모습을 확인할 수 있고, 저항의 구조는 이전과 같다.
마찬가지로 연산증폭기의 특성상 +와 -입력단의 전압이 같을 것이므로 입력단의 전압은 모두 Vin이 된다.
R1에 흐르는 전류는 Vin / R1, 방향은 오른쪽에서 왼쪽이다.
이 전류는 -입력단에서 전류가 출입하지 못하여 온전히 R2를 통해 온 것이므로
Vout의 전압은 아래와 같이 해석할 수 있다.

출력 신호의 부호를 살펴보면 입력 신호와 같으므로 반전되지 않고 표현됨을 알 수 있다.
또한 비반전 증폭기의 경우 저항값의 조절을 통해 입력 신호보다 작은 출력신호를 낼 수 있었지만 비반전 증폭기의 경우 무조건 입력 신호보다 큰 출력 신호를 얻을 수 있다는 것 ! 기억해두자.
비반전 증폭기의 전압 이득은 아래와 같이 나타난다.
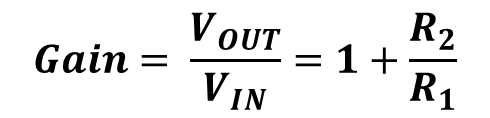
반전과 비반전 증폭 회로는 내가 원하는 신호를 증폭/감쇄하는 용도로 주로 사용된다.
전자회로와 추후 배울 인덕터나 커패시터를 활용하여 무궁무진한 활용처를 보일 것이므로 기본적인 내용부터 잘 숙지해두자.
오늘의 포스팅 끝 ~
'회로이론' 카테고리의 다른 글
| #11. 전력과 전력량 - 파워(Power)와 에너지(Energy) (35) | 2024.06.29 |
|---|---|
| #10-2. 연산 증폭기(OP-Amp) 활용법 - 비교기와 버퍼 (32) | 2024.06.20 |
| #10. 연산 증폭기 (OP-Amp) - 신호 돋보기 (35) | 2024.06.18 |
| #9. 델타-와이 (Δ-Y) 변환 및 증명 - 병렬도, 직렬도 아니라고? (38) | 2024.06.11 |
| #8. 교류(AC)와 직류(DC) - E와 I (MBTI) (34) | 2024.06.09 |



